El Teorema de Bayes es un concepto fundamental en teoria de la probabilidad y estadistica. Fue desarrollado por el matematico y estadistico britanico Thomas Bayes y se utiliza para calcular probabilidades condicionales inversas.
El Teorema de Bayes establece la relacion entre las probabilidades condicionales inversas de dos eventos. La formula general del teorema es la siguiente:
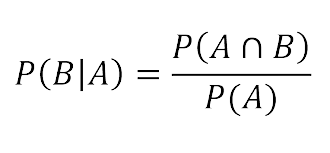
P(A|B) = (P(B|A) * P(A)) / P(B)
Donde:
Supongamos que hay una enfermedad que afecta al 1% de la poblacion. Ademas, se sabe que una prueba medica tiene una tasa de acierto del 95% para detectar la enfermedad en personas que la tienen, pero tambien tiene una tasa de error del 10% para dar falsos positivos en personas que no la tienen.
Ahora, si una persona da positivo en la prueba, cual es la probabilidad de que realmente tenga la enfermedad?
Utilizando el Teorema de Bayes, podemos calcularlo de la siguiente manera:
P(enfermedad|positivo) = (P(positivo|enfermedad) * P(enfermedad)) / P(positivo)
Donde:
Con los valores proporcionados, podemos sustituir en la formula:
P(enfermedad|positivo) = (0.95 * 0.01) / P(positivo)
Ahora, necesitamos calcular P(positivo). Esto se puede hacer considerando las dos posibilidades: tener la enfermedad y obtener un resultado positivo (verdadero positivo) o no tener la enfermedad y obtener un resultado positivo (falso positivo).
P(positivo) = P(positivo|enfermedad) * P(enfermedad) + P(positivo|no tener enfermedad) * P(no tener enfermedad)
En este caso:
Reemplazando los valores:
P(positivo) = (0.95 * 0.01) + (0.10 * (1 - 0.01))
Con los valores de P(positivo) y P(enfermedad|positivo), podemos calcular la probabilidad de tener la enfermedad dado un resultado positivo.
Recuerda que este es solo un ejemplo y que el Teorema de Bayes se aplica en una amplia variedad de situaciones donde se tienen probabilidades condicionales.